ProBO

A framework for using probabilistic programming in Bayesian optimization.

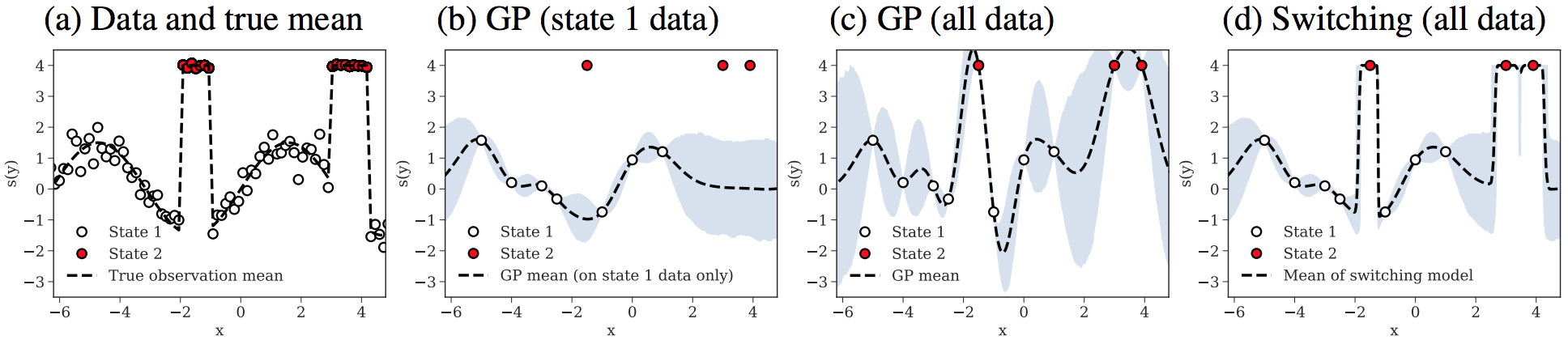
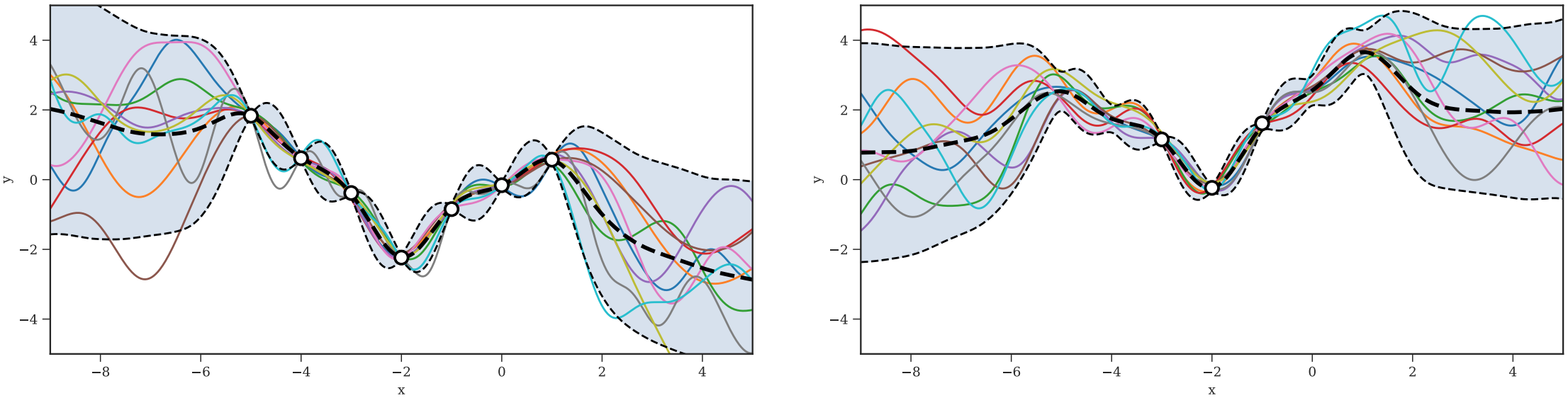
Optimizing an expensive-to-query function is a common task in science and engineering, where it is beneficial to keep the number of queries to a minimum. A popular strategy is Bayesian optimization (BO), which leverages probabilistic models for this task. Most BO today uses Gaussian processes (GPs), or a few other surrogate models. However, there is a broad set of Bayesian modeling techniques that we may want to use to capture complex systems and reduce the number of queries. Probabilistic programs (PPs) are modern tools that allow for flexible model composition, incorporation of prior information, and automatic inference. In this paper, we develop ProBO, a framework for BO using only standard operations common to most PPs. This allows a user to drop in an arbitrary PP implementation and use it directly in BO. To do this, we describe black box versions of popular acquisition functions that can be used in our framework automatically, without model-specific derivation, and show how to optimize these functions. We also introduce a model, which we term the Bayesian Product of Experts, that integrates into ProBO and can be used to combine information from multiple models implemented with different PPs. We show empirical results using multiple PP implementations, and compare against standard BO methods.

Read the Paper

ProBO: a Framework for Using Probabilistic Programming in Bayesian Optimization [paper]. 
Willie Neiswanger,  Kirthevasan Kandasamy,  Barnabas Póczos,  Jeff Schneider,  Eric Xing. 

Get the Code

ProBO is on github.