Embarrassingly Parallel MCMC

Asymptotically exact, communication-free distributed posterior sampling on subsets of data.

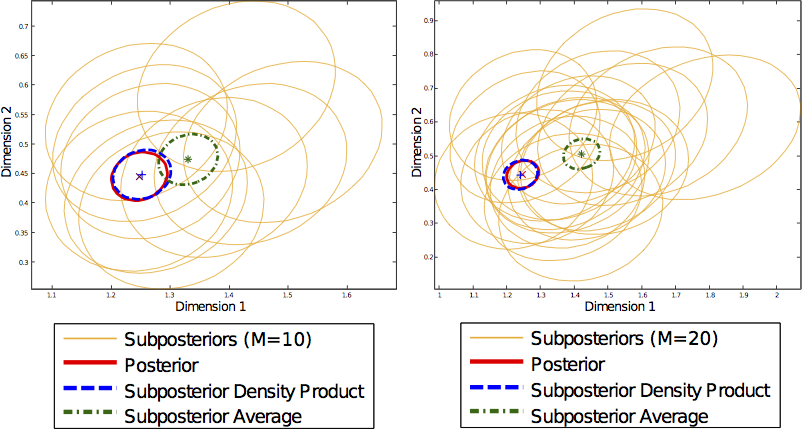
Communication costs, resulting from synchronization requirements during learning, can greatly slow down many parallel machine learning algorithms. In this paper, we present a parallel Markov chain Monte Carlo (MCMC) algorithm in which subsets of data are processed independently, with very little communication. First, we arbitrarily partition data onto multiple machines. Then, on each machine, any classical MCMC method (e.g., Gibbs sampling) may be used to draw samples from a posterior distribution given the data subset. Finally, the samples from each machine are combined to form samples from the full posterior. This embarrassingly parallel algorithm allows each machine to act independently on a subset of the data (without communication) until the final combination stage. We prove that our algorithm generates asymptotically exact samples and empirically demonstrate its ability to parallelize burn-in and sampling in several models.

Read the Paper

Asymptotically Exact, Embarrassingly Parallel MCMC [pdf]. 
Willie Neiswanger,  Chong Wang,  Eric Xing. 
Accepted at UAI 2014.

Get the Code and See Follow-Up Work

See follow-up and citing work here.

For an implementation in R (by Miroshnikov and Conlon), see here.
For an implementation in Matlab (by Guo and Wang), see here.
For an implementation in Python of an improved method involving GPs and active sampling (by de Souza), see here.